Вступ
Монокондилярна артропластика колінного суглоба стабільно продовжує набирати популярності серед ортопедів у всьому світі. У проведенні даного оперативного втручання Швейцарія є лідером серед країн Європи. Остеоартроз колінного суглоба є основним показанням до його виконання.
Найбільш поширеними ускладненнями після монокондилярної артропластики колінного суглоба є нестабільність компонентів ендопротеза, зношування поліетилену та прогресування дегенеративного процесу в іншому відділі суглоба. Нестабільність компонентів ендопротеза є одним з основних ускладнень, чому сприяє прогресуючий остеопороз, здебільшого у літніх жінок [1]. Для профілактики подібних ускладнень нами розроблено методику превентивного укріплення зони опилу великогомілкової кістки шляхом використання двох кортикальних металевих гвинтів.
Мета: провести аналіз математичного моделювання напружено-деформованого стану моделей нижньої кінцівки при різних умовах монокондилярного ендопротезування колінного суглоба. Змоделювати варіанти зміцнення остеопоротичної кісткової тканини під тибіальним компонентом ендопротеза.
Матеріали та методи
У лабораторії біомеханіки ДУ «Інститут патології хребта та суглобів ім. проф. М.І. Ситенка НАМН України» було проведено математичне моделювання напружено-деформованого стану нижньої кінцівки в умовах монокондилярного ендопротезування колінного суглоба. Для виконання поставленого завдання була розроблена базова модель нижньої кінцівки з монокондилярним ендопротезом з медіального боку колінного суглоба (рис. 1).
Базова модель складалася зі стегнової кістки, великогомілкової та малогомілкової кісток, кісткових елементів стопи. Між стегновою та великогомілковою кістками з латерального боку моделювали хрящову прокладку. Монокондилярний ендопротез містив стегновий та великогомілковий компоненти з титану та прокладку з поліетилену.
На базовій моделі вивчали напружено-деформований стан моделі за нормальної щільності кісткової тканини та в умовах остеопорозу. Крім того, моделювали варіанти зміцнення остеопоротичної кісткової тканини під опорною платформою ендопротеза, для чого під нею у великогомілковій кістці проводили два армуючих гвинти в двох варіантах: у фронтальній площині (рис. 2) і в сагітальній площині (рис. 3).
Механічні властивості здорових біологічних тканин (кортикальна та губчаста кістка, хрящ) для математичного моделювання обрано за даними [2–4]. Механічні властивості остеопоротичної кісткової тканини обрано за даними K. Arkuszetal. (2018) [5]. Механічні характеристики штучних матеріалів обирали за даними технічної літератури [6]. Матеріал елементів ендопротеза — титан. Матеріал пари тертя ендопротеза — поліетилен. При моделюванні використовували такі характеристики, як Е — модуль пружності (модуль Юнга), υ — коефіцієнт Пуассона. Механічні характеристики використаних матеріалів наведені в табл. 1.
Для навантаження моделі моделювали масу тіла при одноопорному стоянні (без маси опорної кінцівки), для чого до головки стегнової кістки прикладали розподілену силу величиною 1100 Н [7–12]. Опорна поверхня стопи моделі мала жорстке закріплення. Схема навантаження моделі наведена на рис. 4.
У процесі моделювання вивчали величини напружень та відносних деформацій в елементах моделей. З метою порівняння величин напружень та відносних деформацій між різними моделями були обрані конт-рольні точки. Схема розташування контрольних точок наведена на рис. 5.
Дослідження напружено-деформованого стану моделей виконували за допомогою методу кінцевих елементів. Як критерій оцінки напруженого стану моделей використовували напруження за Мізесом і відносні деформації у відсотках [3].
Моделювання виконували за допомогою системи автоматизованого проєктування SolidWorks. Розрахунки напружено-деформованого стану моделей виконували за допомогою програмного комплексу CosmosM [13].
Результати
На першому етапі роботи вивчали напружено-деформований стан моделі нижньої кінцівки після монокондилярного ендопротезування колінного суглоба в умовах нормальної щільності кісткової тканини. Розподіл напружень у моделі показано на рис. 6.
Проведені розрахунки показали, що за нормальної щільності кісткової тканини максимальні за величиною напруження (10,6 МПа) визначаються в передній зоні великогомілкової кістки під платформою ендопротеза, а також в її задньому відділі, де сягають значення 8,7 МПа. Напруження в протезованому виростку стегнової кістки дещо нижчі, їх значення становлять 6,3 та 5,4 МПа в передній та задній частинах відповідно. На фіксуючих елементах ендопротеза, навпаки, вищі напруження визначаються на ніжці стегнового компонента — 1,9 МПа, тоді як на ніжці великогомілкового компонента напруження не перевищують 0,9 МПа.
Розглянемо, як змінюються напруження в моделі за наявності остеопорозу кісткової тканини. Картину напружено-деформованого стану моделі з монокондилярним ендопротезом колінного суглоба і остеопорозом кісткової тканини наведено на рис. 7.
Як показали результати моделювання, остеопороз кісткової тканини при монокондилярному ендопротезуванні колінного суглоба призводить до зниження рівня напружень у великогомілковій кістці під платформою ендопротеза до рівня 10,2 МПа в її передньому відділі та до 1,6 МПа — у задньому, також зниження рівня напружень до 0,4 МПа визначається і на ніжці великогомілкового компонента ендопротеза. Водночас визначається підвищення рівня напружень у стегновій кістці на протезованому виростку до 8,7 та 9,9 МПа в його передньому та задньому відділах відповідно. На ніжці стегнового компонента ендопротеза також зафіксовано підвищення рівня напружень до 2,7 МПа.
Дані про величини напружень у контрольних точках моделей нижньої кінцівки з монокондилярним ендопротезом колінного суглоба за наявності остеопорозу кісткової тканини та без нього наведені в табл. 2.
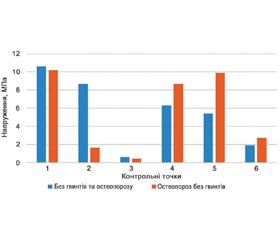
Наочне уявлення про співвідношення величин напружень у контрольних точках моделей нижньої кінцівки з монокондилярним ендопротезом колінного суглоба за наявності остеопорозу кісткової тканини та без нього можна отримати за допомогою діаграми, яка наведена на рис. 8.
Як бачимо на діаграмі, наявність остеопорозу призводить, з одного боку, до підвищення рівня напружень у протезованому виростку стегнової кістки, а з іншого, хоча і знижує рівень напружень у великогомілковій кістці, але призводить до великого дисбалансу в навантаженні між переднім та заднім її відділами під платформою ендопротеза, що може бути причиною його нестабільності.
Однім із варіантів профілактики нестабільності великогомілкового компонента ендопротеза може бути введення армуючих гвинтів у великогомілкову кістку під платформу ендопротеза. Напружено-деформований стан моделі при проведенні армуючих гвинтів у фронтальній площині можна спостерігати на рис. 9.
Результати математичного моделювання наочно показали, що проведення армуючих гвинтів у фронтальній площині практично не змінює напружено-деформованого стану моделі порівняно з моделлю без гвинтів. Про це свідчить і рівень максимальних величин напружень у контрольних точках моделі, які збільшуються на 0,1 МПа в трьох контрольних точках: передній відділ великогомілкової кістки, задній відділ виростка стегнової кістки і ніжка стегнового компонента ендопротеза. В інших контрольних точках змін рівня напружень не визначено.
Картину розподілу напружень у моделі при проведенні армуючих гвинтів у сагітальній площині наведено на рис. 10.
При проведенні армуючих гвинтів у сагітальній площині спостерігаються більш значні зміни напружено-деформованого стану моделі. Так, у великогомілковій кістці під платформою ендопротеза рівень напружень знижується як у передньому відділі, так і в задньому до 9,4 та 1,5 МПа відповідно. На ніжці великогомілкового компонента ендопротеза величина напружень залишається на рівні 0,4 МПа, як і в моделі без гвинтів. Також визначається зниження величин напружень у всіх контрольних точках на стегновій кістці як у кістковій тканині, так і на ніжці стегнового компонента ендопротеза.
Дані про величини напружень у контрольних точках моделей нижньої кінцівки з монокондилярним ендопротезом колінного суглоба за наявності остеопорозу кісткової тканини та армуючими гвинтами наведені в табл. 3.
Діаграма, яка наведена на рис. 11, дозволяє наочно порівняти величини напружень у контрольних точках моделей нижньої кінцівки з монокондилярним ендопротезом колінного суглоба за наявності остеопорозу кісткової тканини та армуючими гвинтами.
Наведена діаграма наочно свідчить про переваги проведення гвинтів у сагітальній площині над їх фронтальним проведенням.
На наступному етапі роботи визначали величини відносних деформацій у колінному суглобі при всіх вищенаведених варіантах монокондилярного ендопротезування. Картину розподілу відносних деформацій у моделях наведено на рис. 12.
Проведене моделювання показало, що за нормальної щільності кісткової тканини при монокондилярному ендопротезуванні колінного суглоба величини відносних деформацій не перевищують 0,1 % у всіх контрольних точках моделі. Наявність остеопорозу призводить до збільшення величин відносних деформацій у великогомілковій кістці під платформою ендопротеза до 0,5 % у передньому відділі і до 0,3 % — у задньому. На ніжці великогомілкового компонента відносна деформація також зростає до 0,04 %. У протезованому виростку зміни величин відносних деформацій менш виражені і зростають у передньому відділі до 0,05 %, а в задньому навіть знижуються з 0,1 до 0,08 %. Ніжка стегнового компонента ендопротеза не піддається додатковим деформаціям порівняно з моделлю без остеопорозу.
Проведення армуючих гвинтів у фронтальній площині не веде до змін величин відносних деформацій у всіх контрольних точках моделі, за винятком ніжки великогомілкового компонента, де рівень відносних деформацій підвищується до 0,05 %. Проведення армуючих гвинтів у сагітальній площині дозволяє знизити рівень відносних деформацій у кістковій тканині заднього відділу великогомілкової кістки до 0,2 %, а на ніжці великогомілкового компонента ендопротеза — до 0,03 %. На зміни величин відносних деформацій у контрольних точках стегнового компонента моделі проведення армуючих гвинтів у сагітальній площині не впливає.
Дані про величини відносних деформацій у контрольних точках моделей нижньої кінцівки з монокондилярним ендопротезом колінного суглоба наведені в табл. 4.
Наочно порівняти величини відносних деформацій у контрольних точках моделей нижньої кінцівки з монокондилярним ендопротезом колінного суглоба допоможе діаграма, яка наведена на рис. 13.
Обговорення
Аналіз результатів проведеного математичного моделювання напружено-деформованого стану моделей нижньої кінцівки при різних умовах монокондилярного ендопротезування колінного суглоба дозволяє говорити про те, що наявність остеопорозу кісткової тканини значно погіршує ситуацію як з розподілом напружень в елементах моделі, так і з величинами їх відносних деформацій. Особливо це позначається на великогомілковому компоненті моделі. Проведення армуючих гвинтів у великогомілкову кістку під платформу ендопротеза дозволяє покращити ситуацію, але тільки у випадку їх проведення в сагітальній площині.
Висновки
1. Наявність остеопорозу призводить до збільшення величин напружень у кістковій тканині, яка контактує з елементами ендопротеза, а також до збільшення величин відносних деформацій як у кістковій тканині, так і в елементах ендопротеза.
2. Проведення армуючих гвинтів у сагітальній площині дозволяє знизити рівень напружень у великогомілковій кістці, а також зменшити величини відносних деформацій у ній. Проведення гвинтів у фронтальній площині не справляє значного впливу на зміни напружено-деформованого стану моделі.
Конфлікт інтересів. Автори заявляють про відсутність конфлікту інтересів та власної фінансової зацікавленості при підготовці даної статті.
Отримано/Received 14.09.2022
Рецензовано/Revised 23.09.2022
Прийнято до друку/Accepted 02.10.2022
Список литературы
1. Zhuk P.M., Movchaniuk V.O., Matsipura M.M. Actual analysis of complicotions after unicompartmental arthroplasty of the knee joint. Visnyk ortopedii, travmatolohii ta protezuvannia. 2020. (1). 101-106. [in Ukrainian]. DOI: 10.37647/0132-2486-2020-104-1-101-106.
2. Березовский В.А., Колотилов Н.Н. Биофизические характеристики тканей человека: Справочник. Київ: Наукова думка, 1990. 224 с.
3. Зенкевич О.К. Метод конечных элементов в технике. Москва: Мир, 1978. 519 с.
4. Хвисюк О.М., Пустовойт К.Б., Пустовойт Б.А., Карпінський М.Ю., Карпінська О.Д. Математичне моделювання умов навантаження колінного суглоба у фронтальній площині. Проблеми безперервної медичної освіти та науки. 2012. № 1. С. 51-56.
5. Arkusz K., Klekiel T., Niezgoda T.M., Będziński R. The influence of osteoporotic bone structures of the pelvic-hip complex on stress distribution under impact load. Acta of Bioengineering and Biomechanics Original paper. 2018. 20(1). 29-38. DOI: 10.5277/ABB-00882-2017-02.
6. Gere J.M., Timoshenko S.P. Mechanics of Material. 1997. 912 р.
7. Карпинский М.Ю., Суббота И.А., Пустовойт Б.А., Тарек Зияд Абдель Азиз Рашеед. Определение влияния вальгусной деформации на напряжения в коленном суставе. Ортопедия, травматология и протезирование. 2008. № 2. С. 31-34.
8. Мителева З.М., Пустовойт Б.А., Пустовойт Е.Б., Карпинский М.Ю., Карпинская Е.Д., Суббота И.А. Математическое моделирование в современной артрологии. Зб. наукових праць XV з’їзду ортопедів-травматологів України. Дніпропетровськ, 16–18 вересня 2010 р. С. 12.
9. Мителева З.М., Снисаренко П.И., Зеленецкий И.Б., Карпинский М.Ю., Яресько А.В. Исследование напряженно-деформированного состояния моделей коленного сустава в зависимости от величины варусной деформации и толщины суставного хряща. Травма. 2015. № 3. С. 33-38. DOI: 10.22141/1608-1706.3.16.2015.80212.
10. Образцов И.Ф., Адамович И.С., Барер И.С. Проблема прочности в биомеханике: Учебное пособие для технич. и биол. спец. ВУЗов. Москва: Высш. школа, 1988. 311 с.
11. Пустовойт К.Б., Карпінський М.Ю. Моделювання умов навантаження колінного суглоба з позицій механіки. Клінічна хірургія. 2013. С. 53-56.
12. Танькут О.В., Філіпенко В.А., Мезенцев В.О., Арутюнян З.А., Тохтамишев М.О., Карпінський М.Ю., Яресько О.В. Математичне моделювання ендопротезування колінного суглоба зі заповненням дефекту кісток імплантатами з різних матеріалів. Ортопедия, травматология и протезирование. 2020. № 1. С. 66-77. DOI: 10.15674/0030-59872020166-77.
13. Алямовский А.А. SolidWorks/COSMOSWorks. Инженерный анализ методом конечных элементов. Москва: ДМК Пресс, 2004. 432 с.

/45.jpg)
/44.jpg)
/46.jpg)
/49.jpg)
/47.jpg)
/50.jpg)
/48.jpg)
/50_2.jpg)